Tandwielmeter , m. (-s), gear measuring instrument , das Zahnradmeßgerät ,
l'appareil (m) mesureur d' engrenage (m)
Meetinstrument voor de bepaling van een karakteristieke grootheid van een tandwiel.
Een probleem bij tandwielen is de gecompliceerde vorm. Deze is weliswaar samengesteld uit elementaire vormen die herhaald voorkomen, repeteren, maar aan het samenstel zijn in de regel nauwelijks twee lijnen evenwijdig. Niet alleen is dat lastig om over te praten, om de vorm te definiëren, het is ook lastig om te meten. Weliswaar is het meetprobleem met de komst van de coördinatenmeter een stuk vereenvoudigd, maar het is ondoenlijk, dus in de praktijk onmogelijk, om een tandwiel voor elk wissewasje op een coördinatenmeter te leggen.
De meest voorkomende tandwielen zijn evolvente tandwielen, dat zijn wielen met tanden waarvan de flanken goeddeels uit een evolvente bestaan. Een evolvente ontstaat door afwikkeling van een cirkel (Fig. 1).
Ook andere tandvormen dan de evolvente komen wel voor, maar dan wel voor speciale toepassingen. Cycloïdale bij voorbeeld, vooral in horloges.
Voor evolvente tandwielen is een aantal karakteristieke grootheden afgesproken, waarmee zij ondubbelzinnig gedefinieerd worden. Daarbij wordt uitgegaan van twee vaste gegevens, het aantal tanden en de steekcirkelmiddellijn.
Het aantal tanden z is vast en geheel.
De steekcirkelmiddellijn d is de middellijn van de steekcirkel, de cirkel waarlangs de afstanden materiaal (van de tanden) en lucht (tussen de tanden) even groot zijn (Fig. 2)1 De steekcirkel is een rekengrootheid; hij is te berekenen, maar niet te meten, en er zit ook geen tolerantie op. Bij een heugel, op te vatten als een tandwiel met een oneindig grote straal, is de steekcirkel ontaard in een rechte lijn en spreekt men van steeklijn.
Op deze gegevens worden de tanddikte, de tandwijdte en de modulus gebaseerd.
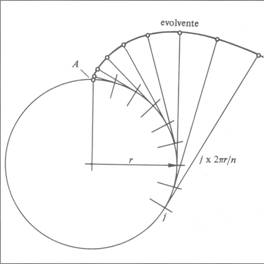
Fig. 1 De constructie van een evolvente.
Een evolvente is de ontwindende van een cirkel. Ter illustratie denke men zich een om de getekende cirkel gespannen touwtje, dat bij A losgenomen wordt en al strak gehouden afgewikkeld wordt. Het uiteinde van het touwtje doorloopt dan de getekende boog, die evolvente heet. Alle overige punten van het touwtje doorlopen trouwens ook evolventen.
Het strakke touwtje is steeds een raaklijn aan de cirkel, met een vrije lengte die gelijk is aan de lengte van de verlaten cirkelboog.
Hierop berust de getekende constructie van de evolvente: De cirkel is verdeeld in een aantal (n) gelijke delen (hier: n = 24). Door de deelpunten zijn de raaklijnen getekend. Uitgaande van A zijn de achtereenvolgende vrije lengten
2 π r/n , 2 x 2 π r/n , 3 x 2 π r/n , …
op de raaklijnen afgepast. De zo verkregen eindpunten vormen samen een evolvente.
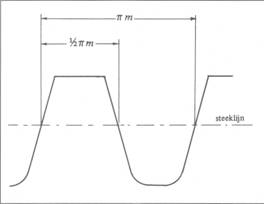
Fig. 2 De plaats van de steeklijn in het profiel van een tandwiel.
Vorige pagina