Nonius , m. (-sen), vernier, der Nonius (-nien) , le vernier
In de zeventiende eeuw door de Portugees P. Nunez of Nonius geïntroduceerde hulpschaal voor de nauwkeurige aflezingvan een analoog meetinstrument, ook indien dat een aanwijzingvertoont tussen twee opeenvolgende deelstrepen van zijn schaal. Door een aan het oog aangepaste combinatie van de beide schalen wordt een trefzekere interpolatietussen de gemarkeerde waarden van de hoofdschaal mogelijk.
De schaalwaardevan een nonius is altijd een klein beetje kleiner dan die van de bijbehorende hoofdschaal, bij voorbeeld 0,1 mm zoals in Fig. 1. Schuiven we de nonius 0,1 mm naar rechts, dan komt noniusstreep 1 juist in het verlengde te liggen van millimeterstreep 1. Nog 0,1 mm verder schuiven, brengt noniusstreep 2 in het verlengde van millimeterstreep 2. De nonius is dan in totaal 0,2 mm verschoven, en de nulstreep van de nonius, tevens de index van het betrokken meetinstrument, ligt juist 0,2 mm rechts van de nulstreep van de millimeterverdeling. Al schuivend komt op een gegeven moment noniusstreep 10 in het verlengde van millimeterstreep 10. De nonius is dan juist een hele millimeter opgeschoven, en alle noniusstrepen hebben op hun beurt in het verlengde gelegen van een millimeterstreep. Heel belangrijk daarbij is dat van de noniusstrepen 0 t/m 9 er nooit meer dan een tegelijk in het verlengde van een millimeterstreep kan liggen.
We kunnen de gang van zaken ook omkeren: We verschuiven de nonius niet over een bekend aantal tienden van een millimeter, maar we meteneen nog onbekende maat en kijken waar de nonius terecht komt.
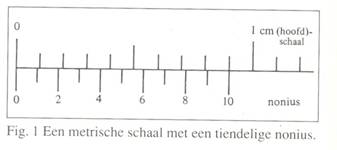
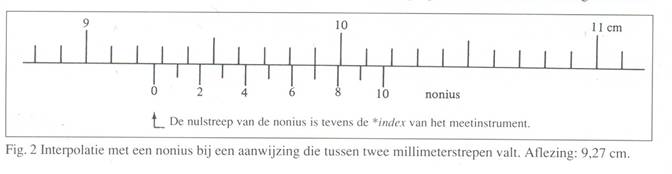
Fig. 2 geeft een voorbeeld van zo'n situatie, waarin de index (dus de nulstreep van de nonius) voorbij 9,2 cm staat. De gemeten maat is dus groter dan 9,2 cm. Hoeveel groter zien we op de nonius: 0,7 mm, want noniusstreep 7 ligt als enige precies in het verlengde van een millimeterstreep.
We hebben nu gezien hoe we een „verschuiving" van een millimeter met een 10-delige nonius kunnen omzetten in stapjes van 0,1 mm. De vraag, die meteen rijst, is waar de grenzen liggen van deze interpolatiemogelijkheid. Zo zou dus een 20-delige nonius goed zijn voor een aflezing van 0,05 mm, en een 50-delige voor 0,02 mm, maar dat we daarmee niet onbeperkt kunnen doorgaan, is duidelijk.
Ter afbakening van de mogelijkheden nemen we om te beginnen de constructie van dit type – meestal schuifmaatachtige – meetinstrumenten in overweging. Die is zo dat daarmee geen nauwkeuriger meting mogelijk is dan tot op 0,01 mm. Ook het geldende comparatieprincipeverzet zich daartegen, als de schuifmaat tenminste niet als dieptemetergebruikt wordt. Dit betekent dat een 50-delige nonius het maximaal zinvolle is. De mogelijkheid dat er geen enkele noniusstreep in het verlengde ligt van een millimeterstreep betekent in dat geval een aflezing die zal eindigen op een oneven aantal honderdsten, met een onzekerheidvan 0,01 mm.
Dit nu heeft twee consequenties. Om te beginnen hebben andere aantallen noniusdelen dan 10, 20 en 50 geen zin, nog afgezien van het feit dat ze onhandig zijn althans voor metrische schalen. Immers, de schaalwaarde van zo'n nonius zou eindigen op onderdelen van 0,01 mm, dus op duizendsten of nog kleiner, waarden waarvan we al vastgesteld hebben dat ze geen betekenis hebben bij het onderhavige type meetinstrument. Verder moet een nonius nog altijd afleesbaar zijn om er wat aan te hebben. Met andere woorden, de genoemde minimale verschillen moeten wel met het oog geconstateerd kunnen worden.
Van het oog is bekend dat het scheidend vermogenin het gunstigste geval 6" kan bedragen, als het erom gaat te constateren of twee strepen in elkaars verlengde liggen. Dan moet de kwaliteit van die strepen wel aangepast zijn, wat wil zeggen dat ze goed scherp en verticaal moeten zijn (lees: evenwijdig aan de ruggengraat van de waarnemer), dat de schalen niet mogen glimmen, dat er geen parallax mag zijn en dat de verlichting naar aard en sterkte goed moet zijn. De onder deze omstandigheden geldende waarde van 6" komt op de conventionele afstand van duidelijk zienovereen met een afstand van 0,007 mm. Deze waarde ligt dicht tegen de genoemde grenswaarde van 0,01 mm aan, dus ook op grond van de eigenschappen van het oog is een 50-delige nonius de limiet.
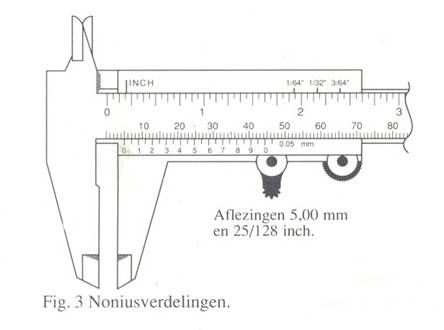Fig. 3 Noniusverdelingen.
Dit vastgesteld hebbend, rest de vraag wat de beste lengte voor een nonius is. Teruggrijpend op Fig. 1 zien we dat een kortere nonius dan 9 mm geen zin heeft. Een langere zou wel kunnen bij een 10-delige nonius, bij voorbeeld 19 mm. De schaaldelen worden dan echter al zo groot, 1,9 mm, dat er gemakkelijk een extra deelstreep tussen kan waarmee de afleesnauwkeurigheid „gratis" verdubbeld wordt. Jets dergelijks geldt voor 29 mm lengte, met de kanttekening dat daarbij een nonius met 10 schaaldelen niet meer past omdat die schaaldelen groter zijn dan 2,5 mm. Het overzicht van de Schaal, nodig om ondubbelzinnig te kunnen besluiten welke strepen precies in elkaars verlengde liggen, gaat daarbij verloren, wat onnauwkeuriger aflezingen tengevolge heeft. Dit hangt weer samen met de eigenschappen van het oog.
Dus, een 10-delige nonius past bij 9 mm schaallengte. Soortgelijke overwegingen leiden voor een 20-delige nonius tot schaallengten van 19 mm, 29 mm en 39 mm. Voor een 50-delige nonius komen we zo uit op een schaallengte van 49 mm. Ook grotere lengten, tot 99 mm, zijn in dit laatste geval niet principieel uitgesloten. Die stuiten echter op het praktische bezwaar dat een daarmee uitgerust meetinstrument onnodig lang wordt. Immers, de lengte van zo'n instrument is gelijk aan het meetgebiedplus de lengte van de nonius.
Hoe groot het aantal schaaldelen van een decimale nonius ook is, steeds loopt de becijfering daarvan van 0 tot 10 (waarbij deelstreep 10 ook wet met een 0 gemarkeerd wordt). De onderverdeling is verder zo logisch, dat de aflezing bijna spontaan goed gaat. De Figuren 2 en 3 geven hiervan voorbeelden.
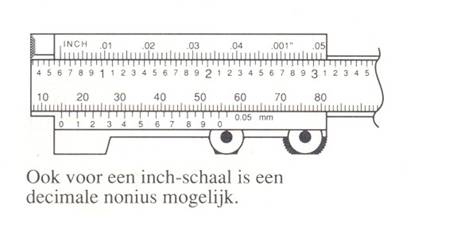
In het bovenstaande is opgemerkt dat andere aantallen schaaldelen voor de nonius dan 10, 20 en 50 onhandig zijn voor metrische schalen. Dat geldt duidelijk niet voor inch-schalen, waarbij een verdeling van de nonius in veelvouden van 8 schaaldelen meer voor de hand ligt. Verder geldt daarvoor een soortgelijke redenering. Ook een decimale verdeling van inches is echter mogelijk, zoals uit Fig. 3 blijkt.
Vorige pagina