Abbe-comparatieprincipe, o. (geen meervoud) Abbe (comparator) principle;
Abbe principle of comparison, der Abbesche Grundsatz;, das Abbesche Komparatorprinzip
le principe d'Ahhe; le principe de mesurage (m) par comparaison (v) d'Abbe
Comparatieprincipe dat dateert van omstreeks 1890 en dat sterke overeenkomst vertoont met dat van een longitudinaalcomparator. Het bijzondere is dat, op aanwijzing van Abbe, de onbekende lengte en de lengtestandaard in elkaars verlengde geplaatst zijn. Deze situatie is getekend voor een tweetal streepmaten die, liggend op een meettafel, tegelijkertijd elk onder een *microscoop worden doorgeschoven (Fig.1).
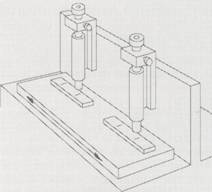
Fig. 1 Het principe van de longitudinaalcomparator volgens Abbe.
Een nadeel van deze opzet is de grote bouwlengte van zo'n comparator, nl. in principe tweemaal zo lang als de grootste te meten lengte. Toch is er iets bijzonders aan dit principe, wat maakt dat we het genoemde nadeel op de koop toe nemen.
Het bijzondere blijkt, als we de invloed nagaan van geleidingsfouten op het meetresultaat.
Voor de verkorting Al volgt
∆ʅ= –ʅ(1 – cos ß ) =
= – ʅ { 1 - ( ß2 / 2! + …)}≈
≈ - ½- ʅ ß2
waarin cos B in een reeks is ontwikkeld (zie *wiskundige betrekkingen).
We zien hieruit dat gewoonlijk lastig te bestrijden geleidingsfouten hier aanleidng geven tot tweede ordeafwijkingen in de meetresultaten. Verwaarlozing van dergelijke afwijkingen heeft in de dagelijkse praktijk van de lengtemeettechniek geen nadelige invloed op de nauwkeurigheid van het meetresultaat.
Voordelen ten opzichte van de transversaalcomparator zijn de universele toepasbaarheid van het meetinstrument, en de vaste afstand van de microscopen of de opnemers.
Als door een verplaatsing van de meettafel het juk, dat de microscoop (of de opnemers, in een andere opzet van de meetopstelling) draagt, doorbuigt, treedt een eerste ordeafwijking op net als bij de transversaalcomparator. Dat is echter goed te voorkomen door het juk voldoende stijf te maken.
Al met al verdient voor lengtemeetopstellingen het bouwprincipe volgens Abbe immer de voorkeur, omdat dat de nauwkeurigst mogelijke lengtemeting garandeert. Pas als dat principe voor eendimensionale gevallen in de praktijk niet kan worden uitgevoerd, komt een van de andere genoemde principes in aanmerking. In meerdimensionale gevallen kan de toepassing van het Eppenstein-principe een oplossing bieden.
Voorbeelden van de longitudinaalcomparator volgens Abbe zijn:
Een schroefmaat. De schroefspil fungeert hier als lengtestandaard. De daaromheen liggende trommel of welk andere indicatiemechanisme ook dient alleen voor de maataanwijzing, en voor interpolatie tussen twee opeenvolgende maatstrepen.
Een als dieptemeter gebruikte schuifmaat. Een gewone schuifmaat is voor wat betreft meting tussen de bekken een longitudinaalcomparator. Als dieptemeter gebruikt is diezelfde schuifmaat een principieel nauwkeuriger Iongitudinaalcomparator volgens Abbe. Dit is dus tevens een voorbeeld van een instrument of opstelling waarin meer dan een comparatieprincipe voorkomt.
Een meetklok, en ook een elektronische taster, analoog aan wat hierboven bij de schroefmaat is opgemerkt. En dan bedoelen we wel het meetinstrument op zichzelf, want toegepast in een statief komen we al gauw uit op een transversaalcomparator.
Een laserinterferometer, mits juist opgesteld. In het instrument zelf is het Abbe-principe goed herkenbaar. Bij de opstelling van het instrument moeten we echter op onze hoede zijn. Het vraagt bijna, juist door zijn handzaamheid en universele toepasbaarheid, om een „leuk plekje" net als het bij de longitudinaalcomparator genoemde coördinatenmeetsysteem. Maar dat plekje is meestal niet het beste, omdat daarbij doorgaans het Abbe-principe verlaten is en we ongewild bij een van de andere comparatieprincipes beland zijn.
De zogenoemde Abbe-lengtemeter, een lengtemeetinstrument waarbij het bouwprincipe van Abbe in pure vorm is gerealiseerd.
Uit deze voorbeelden wordt duidelijk dat we onderscheid moeten maken tussen het eigen principe van een meetinstrument, en het comparatieprincipe van dat meetinstrument toegepast in een bepaalde meetopstelling. Vaak zullen we dan ook te maken hebben met een combinatie van principes.
Vorige pagina